reading_notes

Read: Trees

Types of trees in this reading notes

Binary Trees, Binary Search Trees, and K-ary Trees

Common Terminology

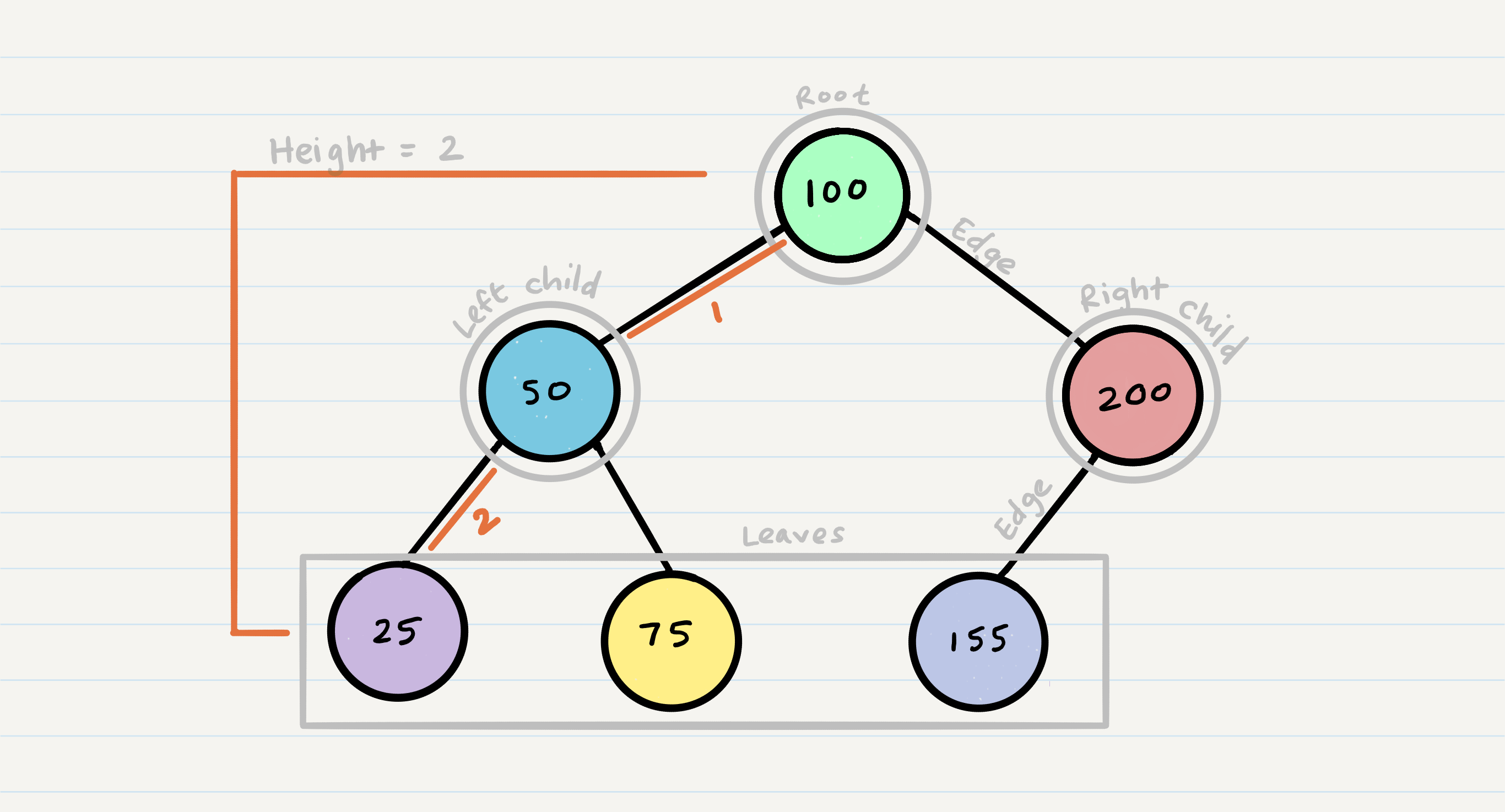
Node - A Tree node is a component which may contain it’s own values, and references to other nodes Root - The root is the node at the beginning of the tree K - A number that specifies the maximum number of children any node may have in a k-ary tree. In a binary tree, k = 2. Left - A reference to one child node, in a binary tree Right - A reference to the other child node, in a binary tree Edge - The edge in a tree is the link between a parent and child node Leaf - A leaf is a node that does not have any children Height - The height of a tree is the number of edges from the root to the furthest leaf Level - the location of the node in reference to base / root (level 0) Parent, Siblings, ancestors , internal nodes , external nodes: all of that used to name a relationship between nodes

Sample Tree

Traversals

Simple Example :

Pre-Order(root - left - right)
In-Order (left - root - right)
Post-Order (left - right - root)

Better example and the flow of these three orders:

Pre-Order

In-Order

Post-Order

Queue-Binary-Tree

Show how we scan(visit) each node in pre-order and with each parent pop(dequeue) it and grap (enqueue) the one/two childs then continue scan until pop/print all nodes as in picture

K-ary Trees

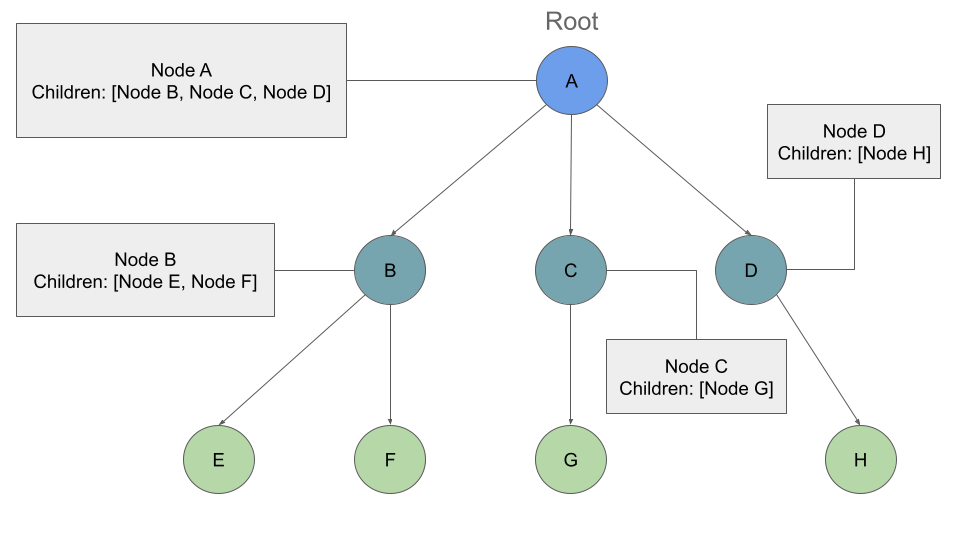
If we traversed this tree Breadth First we should see the output:

Output: A, B, C, D, E, F, G, H

We will still start at the root Node, and we will add it to our queue:

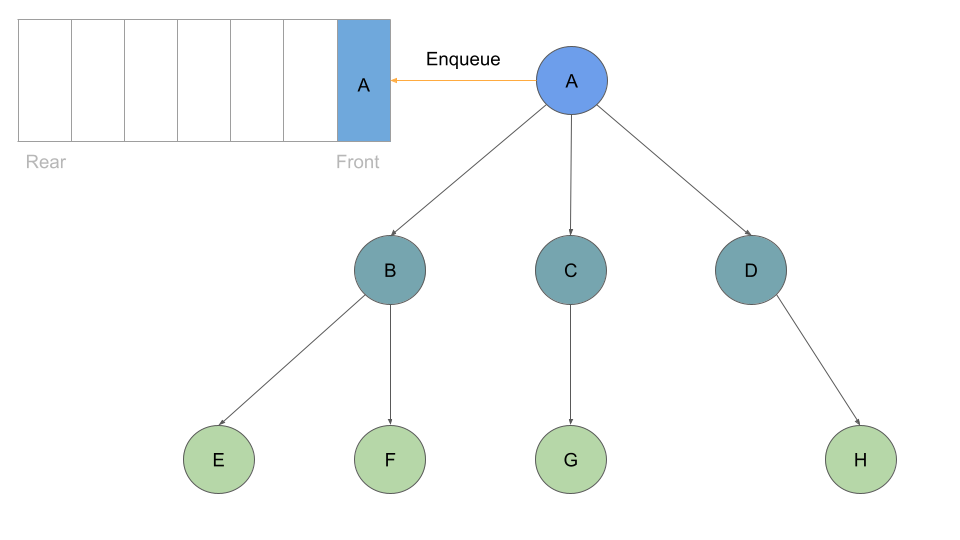
With every Node we dequeue, we check it’s list of childre and enqueue each one:

Binary Search Trees

Searching a BST can be done quickly, because all you do is compare the node you are searching for against the root of the tree or sub-tree. If the value is smaller, you only traverse the left side. If the value is larger, you only traverse the right side.

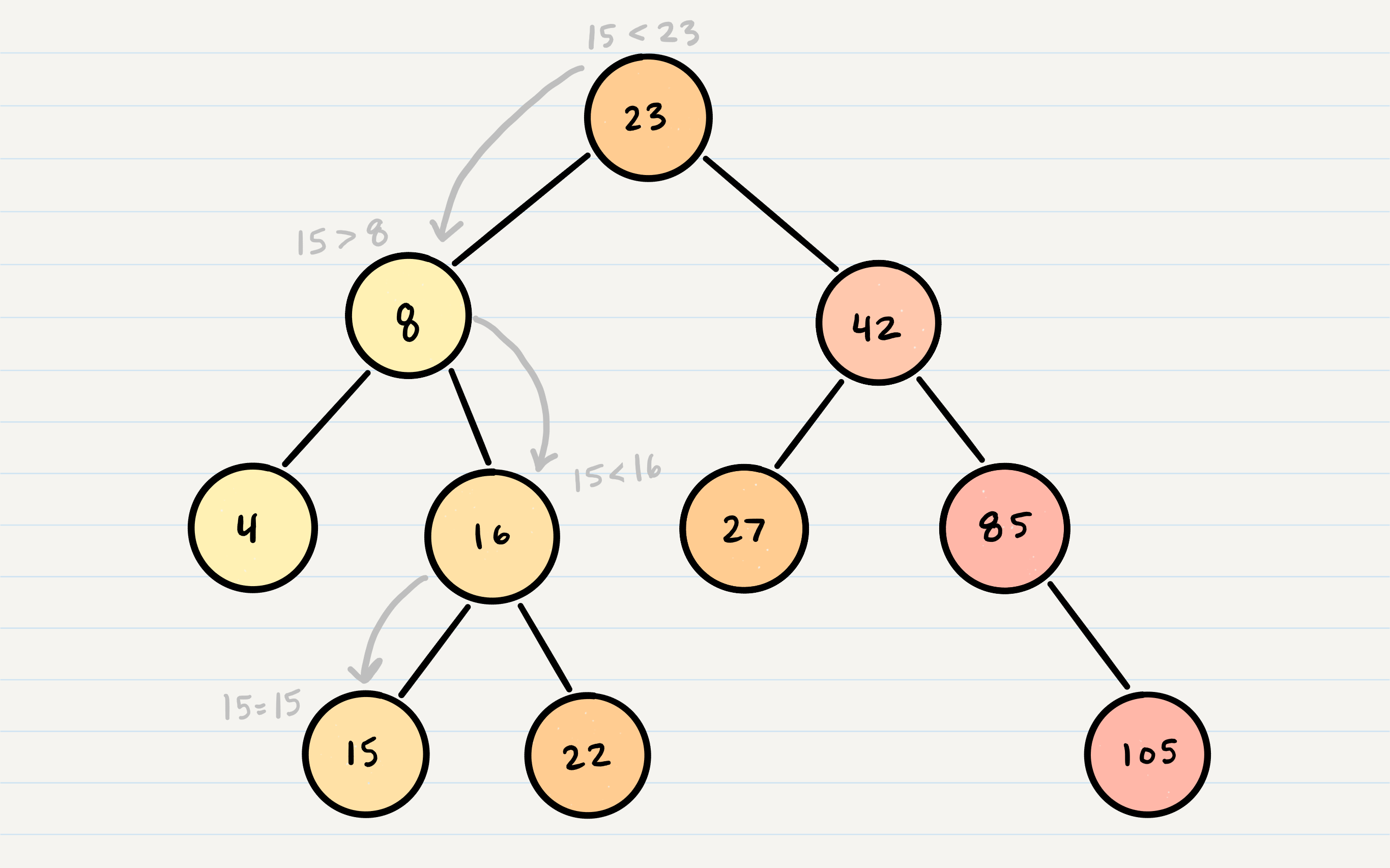
Let’s say we are searching 15. We start by comparing the value 15 to the value of the root, 23.

15 < 23, so we traverse the left side of the tree. We then treat 8 as our new “root” to compare against.

15 > 8, so we traverse the right side. 16 is our new root.

15 < 16, so we traverse the left side. And aha! 15 is our new root and also a match with what we were searching for.

Big O

In a balanced (or “perfect”) tree, the height of the tree is log(n). In an unbalanced tree, the worst case height of the tree is n,
The Big O space complexity of a BST search would be O(1).

References:

https://codefellows.github.io/common_curriculum/data_structures_and_algorithms/Code_401/class-15/resources/Trees.html
A lot of youtube videos